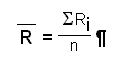
Zur Startseite Radioaktivität   Zur Homepage

Auch bei Nukliden mit langer Halbwertszeit schwanken die Zählraten Ri zufallsbedingt.
Für n Messversuche wird ein Mittelwert

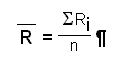
berechnet.

Abweichungen vom Mittelwert

Die Messwerte der Einzelversuche weichen häufig vom Mittelwert nach unten oder oben ab. Bei höheren Zählraten kann es vorkommen, dass der berechnete Mittelwert bei keiner Messung tatsächlich auftritt.

Für unabhängige z.B. zeitlich verteilte Ereignisse wie beim Kernzerfall kann eine POISSON-Verteilung der Zählraten angenommen werden. Als mittlere Schwankung oder Standardabweichung s wird die Abweichung von Messwerten vom Mittelwert bezeichnet, die nur bei einem Bruchteil von   Messwerten überschritten wird. Das heißt 63 % der Zählraten liegen innerhalb des 2s breiten Intervalls von ± s um . Für die Standardabweichung bei der Poissonverteilung gilt:

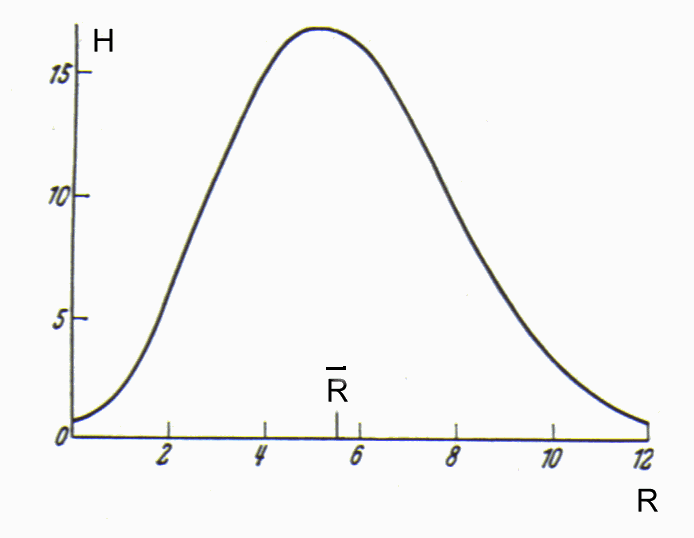
Die Standardabweichung wird als Maß für die Zuverlässigkeit einer Messung gewertet. Hier die Kurve einer Poisson-Verteilung für ca. 100 Messungen. Nach rechts sind die Zählraten R und nach oben deren Häufigkeit aufgetragen.

Zählrate Sand: 88 CpM brutto

Zählrate Untergrund: 37 CpM

Zählrate Sand netto: 51 CpM

Mittelwert der Messungen: CpM =  63 CpM

= =

  s = 8 CpM

Die Zählrate netto entspricht

51 CpM : 8 CpM = 6 mal der einfachen Standardabweichung und ist damit gut verlässlich.

Mit dem Radiation Alert Inspector ® wird eine Reihe von möglichst vielen Einzelmessungen (n > 30) von einem Präparat mit niedriger Aktivität aufgenommen, mit dem Zeder â -Adapter in den PC eingelesen und in EXCEL ® zur Auswertung importiert.

Als Präparat eignet sich z. B. Pottasche (Kaliumkarbonat, Packungsinhalt 15 g), das als radioaktiven Anteil K-40 enthält. Bei geschlossener Verpackung kommt man auf Zählraten von bis zu ca 450 CpM. Das Präparat ist problemlos erhältlich und weist mit 1,28 · 10⁹ a Halbwertszeit für die gesamte Versuchsdauer genügend Konstanz in der Zerfallsrate auf. Ähnliche Ergebnisse erhält man mit Granit, Tuffstein oder Urangläsern... Präparate mit kurzen Zerfallszeiten (bis einige Tage) sind ungeeignet. Die Untergrundstrahlung tut's im Prinzip auch aber man braucht wegen der Torzeit von mindestens einer Minute sehr lang für eine komplette Messreihe von ca. 500 Einzelwerten. Die erste hier vorliegende Messung wurde mit einem Pechblendepunktstrahler (Korndurchmesser ca. 1mm; Zählrate über 3000 CpM) durchgeführt. 

Was kommt heraus?

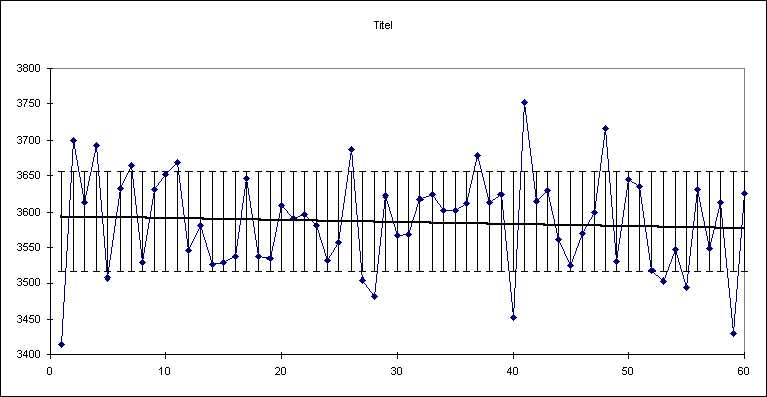
Abb. 2 zeigt die Messwerte in ihrer zeitlichen Reihenfolge. 

Die Achse für die Zählrate ist verkürzt. 16 der 60 Werte liegen außerhalb des ±s - Intervalls. Das sind mit 27% deutlich weniger Messwerte als es nach den Regeln der  Poissonverteilung sein dürften. Es werden nun in EXCEL ® Intervalle von Zählraten definiert und die Häufigkeit festgestellt, mit der Zählraten in den einzelnen Intervallen auftreten. Die Intervallbreite ist einstellbar.

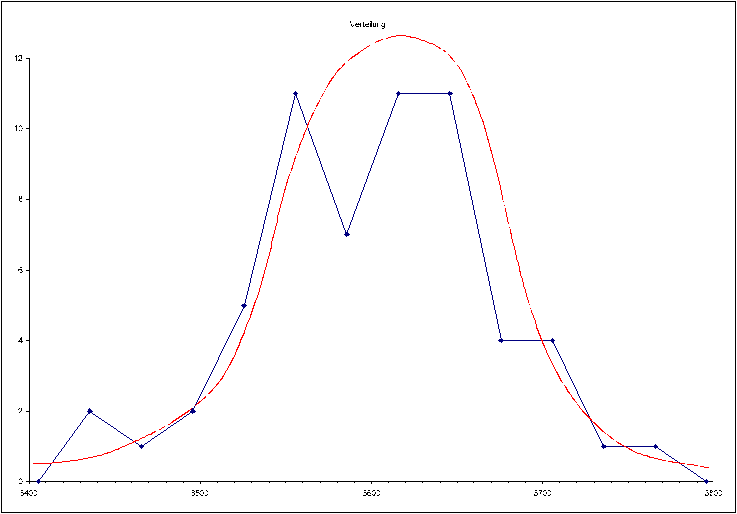
Für eine Intervallbreite von 30 CpM kann man in Abb. 3 die Poisson-Kurve aus Abb. 1 erahnen (rot). Bei Intervallbreiten unter 10 CpM treten in vielen Intervallen Ausfälle auf, weil die Anzahl von Einzelmessungen für diese hohen Zählraten auf die Intervalle bezogen zum großen Teil viel zu gering ist.

Wenn das Ergebnis die Glockenkurve sein soll, dann muss man folglich viele Messungen mit geringen Zählraten durchführen. Das ist beim folgenden Versuch eher der Fall.

 
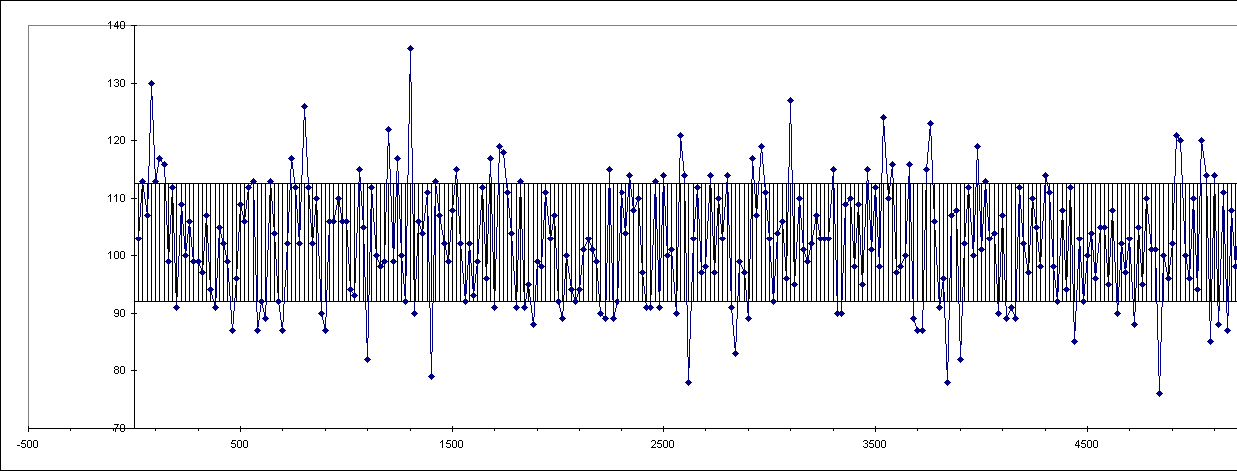
Abb 4a: Über 250 Mesungen bei niedrigerer Zählrate in zeitlicher Auflösung

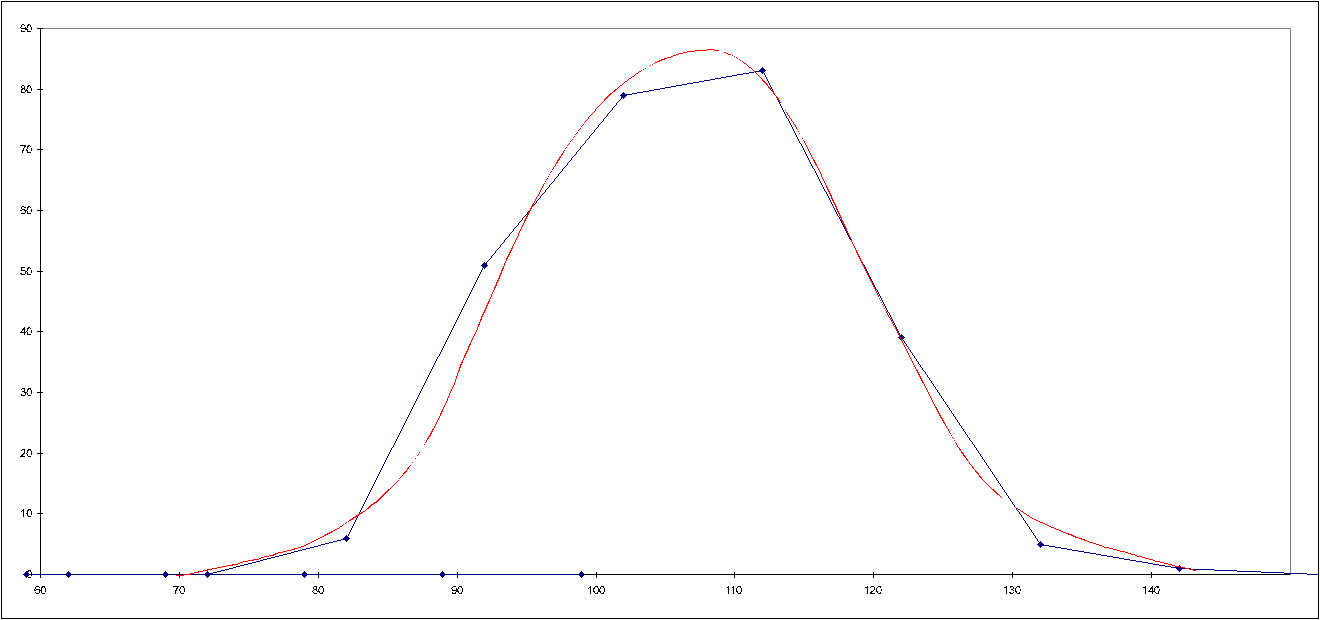
Abb 4b: Über 250 Mesungen bei niedriger Zählrate - Häufigkeit gegen Zählratenintervall

Hier wurden die Richtlinien bezüglich geringer Zählrate und langer Halbwertszeit berücksichtigt. In über 250 Einzelmessungen von je 20 s Dauer wurden die Zählraten über Pottasche bestimmt. Die Intervallbreite in der Darstellung ist 10 CpM. Das gibt ein gutes, an die Glockenkurve angenähertes Ergebnis.

Man kann kein allgemein passendes Verfahren zum Erhalt einer Glockenkurve präsentieren, weil die statistischen Abweichungen nicht von vornherein einplanbar sind. Aber, je mehr Messungen mit niedrigen Impulsraten durchgeführt werden, desto besser liegen die Ergebnisse am theoretischen Verlauf der Poissonkurve.

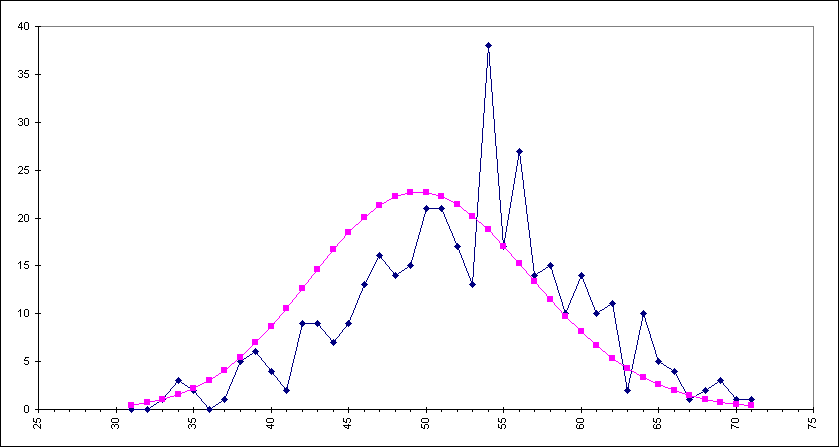Abb. 5: Grafik der Häufigkeitsverteilung von 375 Einzelmessungen

Eine weitere Messung über Pottasche mit auf 10 Sekunden verringerter Torzeit und 375 Einzelmesswerten ergab folgendes Resultat:

Es wurde jede Zählrate einzeln berücksichtigt. Zum Vergleich die theoretisch berechnete Poisson-Kurve.

Mit noch mehr Einzelmessungen kann das Ergebnis noch besser an die vergleichende Poisson-Verteilung angenähert werden, vor allem dann, wenn die Zählrate noch ein wenig gesenkt wird (Zwischenlage von OHP-Folie und Verkürzung der Torzeit). Das Ergebnis von 551 Einzelmessungen von je 10s Torzeit und der Weg wie man zu so einer Auswertung kommt, wird in den Handreichungen zum Auswerten von Versuchsreihen mit EXCEL gezeigt und erläutert.

Die hier verwendeten Messreihen, die mit Inspector und Zeder aufgenommen wurden können Sie als ZIP-Datei herunterladen (93KB) und daran das Auswerten selbst ausprobieren.

Versuche zur Umweltradioaktivität - Messen mit dem Computer - Zur Statistik des Kernzerfalls und anderer Messungen
(c) 2001 J. Grzesina

An den Seitenbeginn   Zur Startseite Radioaktivität   Zur Homepage